Sinusoidal maps

General hints
Drawing nice maps
Sinusoidal maps

Making sinusoidal maps

Today we will learn how to paint landscapes with happy little trees. Wait, no. We'll look at how to make one of the only real projections I know how to do, the peeled orange, or as we cartographers call it, the sinusoidal.

This projection is not so pretty, but it has about as little distortion as you can get on a flat map. This is because the individual spears (the triangles representing a swath of longitudes) are not distorted into rectangles, but retain their triangular shape.

Materials: You will need pencil and paper and/or a computer; a calculator; a good idea of where your continents are; and an orange.

Look, you just have to have pictures turned on for this

The mathematics

Skeleton of a spear The basic math of the projection is simple enough. Let's look at one half-spear, 45^o in width. (You can use any width, of course, up to the entire circumference of the planet.) The entire globe will be made of eight of these spears.

Choose a drawing width for your spear, based on the size of the paper or image. If you're using an 8 1/2 x 11" sheet of paper, these 45^o spears can be up to 11 / 8 = 1 3/8". (1.25" is easier to measure. 3.4 cm also works, though if you have A4 paper you can use 3.5 instead.)

(In case it's not clear, the long axis of the map is the planet's equator; since this is 360^o, there are 360/45 = 8 spears total, and I am making the spears as wide as possible to fit within the paper. Make adjustments as necessary for different sized images.)

A spear goes from pole to pole, that is, half the circumference of the planet. If the spears are 1.25" wide, 10" total, then the spears are 5" tall, and the half-spears are 2.5" tall. At left is the skeleton for one spear, with these measurements. (I'm using Photoshop Elements, which allows you to draw in inches; you can of course measure everything in pixels instead.)

If you chose a different degree width, the spears would be narrower, but about the same height. E.g. if you choose 30^o spears, you'd have 12 spears, each 7/8" wide, for a total width of 10.5"; so each spear would be 5.25" tall.

With curve With measurements Now comes the clever bit. The sides of the spears are not straight; they're curved. And the curve obeys a simple rule: the width at any degree of latitude x is cos x times the width at the equator. Let's work that out for increments of 10^o and a spear width of 1.25":

x	cos x	Spear width
0^o	1.0	1.25"
10^o	.984	1.23"
20^o	.940	1.17"
30^o	.866	1.08"
40^o	.766	.96"
50^o	.643	.80"
60^o	.500	.63"
70^o	.342	.43"
80^o	.174	.22"
90^o	0	0"

At right I've drawn the spear, with the width at each 10^o latitude shown. Next I simply connected the edges of these lines, by eye, with a smooth curve.

Assembling the spears

Duplicate this basic shape eight times, and you have this bristly little map of the world: A world of spears

This map won't be very easy to read (it's hard for the eye to connect land masses across spears), but it has two respectable advantages:

It's almost distortion-free. Even if you don't use it as your basic map, it's useful to have around (with your continents drawn on it, of course) to remind yourself what land areas look like without distortion.
As a corollary of the above, you can make it into a globe. This is how many commercial globes are made, in fact. Cut around the edges of the spears (leaving them connected at the equator) and tape the edges, and you have a little paper globe of your planet. (Or make a map whose equator matches the circumference of a ball; then you can paste the spears on the ball, for a less delicate globe. Do this with a copy of the map; this is a trickier crafts project than it sounds.)

Combining spears

To show off your continents, you simply combine spears as needed. Below, for instance, I've combined three half-spears in the northern hemisphere, and two in the southern. Naturally, you combine spears so that a continental mass can be shown in one section, leaving the orange-peel cuts as oceanic as possible. In the sample map at the top I've combined up to four and a half half-spears.

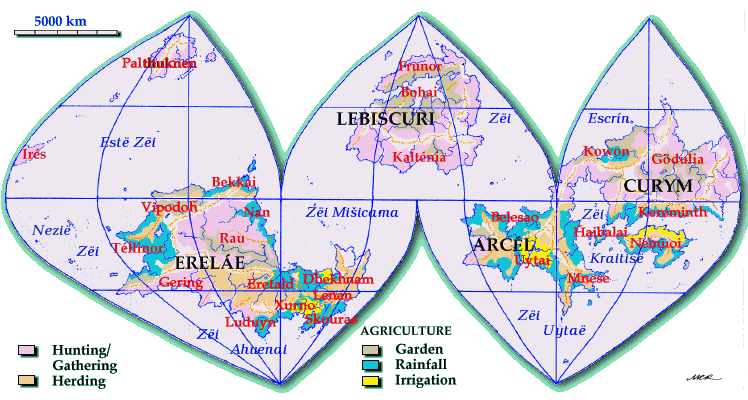
Note that when combining an even number of spears, the longitude in the middle is straight. This is true of any spear, actually; in the first map I simply didn't draw this longitude. A straight longitude is free of distortion, so it's best if you can cut the orange such that a straight longitude goes through the center of each continent. In the sample map I chose to have the straight longitude go throught the 0^o line (not marked, but it's the one that passes through Eretald).

To combine a number of spears you'll have to re-measure the latitude lines. For instance, the first three latitude lines in the table above were 1.23", 1.17", 1.08". If you're combining two spears, these are doubled: 2.46". 2.34", 2.16". If you're combining three spears, triple them: 3.69", 3.51", 3.24"; and so on.

I've talked about drawing the spears and then combining them for ease of exposition. In practice, of course, it saves time to decide which spears you are combining ahead of time

You can, if you like, combine all the spears. Here, the length of each latitude line x is just the equator times cos x. The resulting map gets rid of the orange-slice appearance, but the left and right edges do end up pretty stretched out.

When you're done with your map, you can eat the orange.