All about e

I recently read Richard Feynman’s Lectures on Physics, vol. I, and he explained something that none of my professors ever did— an equation he calls an "amazing jewel".

So I thought I’d tell you about it. You can read Feynman yourself, of course— it’s chapter 22— but he was talking to college physics students, and I’m not going to assume you know anything more than high school math. Plus it’s no longer 1963, so I’ll assume you have a calculator, or access to Wolfram Alpha.

The derivative of e^x

Let’s start with the number e, which starts

2.718281828459045235360287471352662497757247093699959574966967...

You’ll probably remember e as the base of natural logarithms. But before we get to logarithms, e has some remarkable characteristics.

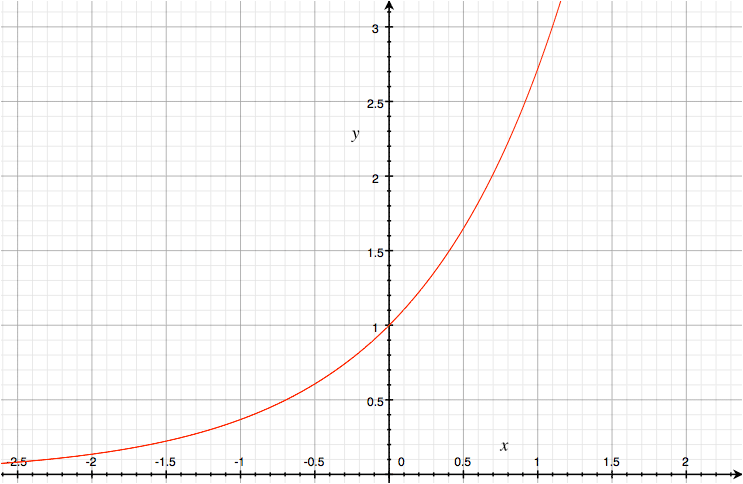
To see one of them, let’s look at the function y = e^x.

What’s its derivative? We can guess by figuring out the slope at a few points, for instance at x = 1. The slope for a straight line between points x₁, y₁ and x₂, y₂ is (y₂-y₁)/(x₂-x₁).

We can approximate the slope for the graph by picking two points very close together— say 1.0 and 1.0001. e¹ is of course e ≅ 2.7182818, while e^1.0001 is ≅ 2.7185537.

Note: We’re going to be seeing a lot of irrational numbers here. If you see ≅ (approximately equal), that’s a reminder that I’ve truncated the number, which really goes on forever.

So the slope is

(2.7185537 - 2.7182818) / (1.0001 - 1) ≅ 2.718417747

Which is close to e. Let’s try a better approximation of the slope, by choosing x₂, y₂ closer to 1:

(e^1.000001 - e¹)/ .000001 ≅ 2.718283188

Which is even closer to e. It’s beginning to look like the slope at e¹ is e¹, and in fact it is. You can verify all of these at Wolfram Alpha; e.g. copy and paste ((e^1.000001) - (e^1))/.000001. See what happens if you use closer and closer points.

Let’s try e⁰, whose value is 1.

(e^0.000001 - e⁰)/.000001 ≅ 1.000000500

How about e² ≅ 7.3890560989?

(e^2.000001 - e²)/.000001 ≅ 7.389059793

How about e^π ≅ 23.14069263?

(e^π+.000001-e^π)/.000001 ≅ 23.140704203

As these examples suggest, the slope of e^x at any point is e^x. That is, the derivative of e^x is itself.

d/dx e^x = e^x

This is the only function of x whose derivative is itself. That makes e^x very nice to work with in calculus— we’ll get back to that later.

Interested in defining e

e was originally calculated by Jacob Bernoulli by evaluating the limit

You have a dollar in an account that pays 100% interest in one year; after the year you’ll have $2.

Suppose it’s 50% every 6 months, instead. Now you get $1 × 1.5 × 1.5 = $2.25.

If there are n intervals, the interest is 100%/n... that is, 1/n. Plus you keep the principal, so you have 1 + 1/n. E.g. for one month it’s 1 + 1/12 = 108.33% and after the year you have

(1 + 1/12)¹² ≅ 2.61303529

Compounding daily, at 0.2739726%, gives us

(1+(1/365))³⁶⁵ ≅ 2.714567482

That’s starting to look like e, and if we keep making smaller and smaller divisions, that’s exactly where we end up.

Logarithms

To most people logarithms probably mean "mumble math something", so think of them as exponents, or order of magnitude. If you ask what order of magnitude a million is, you are in fact asking for log₁₀ 1,000,000 = 6.

We use logarithmic scales all the time; they’re great for reducing enormous ranges of huge numbers to easy-to-grasp small numbers. Some common examples:

decibels: if a sound is ten times louder than another one, it’s 10 decibels higher
the Richter scale: an earthquake 1.0 higher on this scale has 10 times the amplitude
stellar magnitude: if one star is 100 times brighter than another, that’s 5 magnitudes
the computing abbrevations kilo, mega, giga, tera, peta are a logarithmic scale— each step is 1024 times the last one

As a refresher, if a^b = c, then a = ^b√c, and b = log_a c. For instance, 10³ = 1000, so 10 = ³√1000, and 3 = log₁₀ 1000.

Since we normally use base 10, base 10 logarithms are particularly easy.

Log₁₀ 1000 = 3— just count the zeroes.
Log₁₀ 10⁴⁵ = 45.
Log₁₀ .001 = -3; count the places after the decimal point.

For centuries the most useful thing about logs was that they made for easy multiplication of large numbers. E.g. you want to multiply 3.14159265 by 2.7182818. That works out to

3.14159265 ×2.7182818 ----------------- 2513274120 3141592650 251327412000 629318530000 25132741200000 31415926500000 2199114855000000 6293185300000000 ----------------- 8.539734123508770

Not difficult, but tedious and error-prone. But we can take advantage of the fact that

log ac = log a + log c

We can look up the logs in a table... tables to 14 decimal places have been available since 1620.

log₁₀ 3.14159265 ≅ .497149872
log₁₀ 2.7182818 ≅ .434294477
sum ≅ .93144434955

Now we can use the same table to find out what number this is the log of, which turns out to be ≅ 8.53973412.

Of course, these days we do nothing of the sort— we just use a calculator. But it was a huge time saver until the computer was invented.

(Some of you retro-geeks may say "No, no, people used slide rules." What do you think a slide rule is? Among other things, it’s a couple of logarithmic scales.)

One weird trick

There’s an interesting trick for taking powers of 1/n with higher and higher n. Let’s look what happens with e^1/n, doubling n each time. (Or to put it another way, take e, then √e, then the square root of that, and so on.)

1/n e^1/n 1 + 1/n

1 2.7182818 2

1/2 1.648721271 1.5

1/4 1.2840254 1.25

1/8 1.133148453 1.125

1/16 1.06449446 1.0625

1/32 1.0317434075 1.03125

1/64 1.015747709 1.015625

1/128 1.007843097 1.0078125

1/256 1.003913889 1.00390625

1/512 1.00195503 1.001953125

1/1024 1.000977039 1.0009765625

1/2048 1.000488400 1.00048828125

If you’re thinking "Oooh, the limit of e^1/n is 1", that’s correct, but that’s not the weird trick. The trick is that a good guess for e^1/n is 1 + 1/n, and it’s an increasingly good guess as n gets huge.

We’ll use this trick in a clever way in a moment, but I’ll also point out two things.

This particular series is important if you want to calculate logarithms by hand. See Feynman’s lecture if you want to know how.
You may hear that e is a "convenient" base for logarithms. One thing that means is that this particular neat trick is made easier if your base is e. If it’s 10 instead, the trick involves another step: a good guess for 10^1/n is 1 + 2.3026 * (1/n). We get rid of the constant by using base-e logarithms.

What about e^ix?

Now, all of the algebraic operations— addition, multiplication, exponentiation, and their inverses subtraction, division, taking a root, finding a logarithm— should work on any number, so long as we’ve defined ‘number’ broadly enough. It turns out that complex numbers are as far as we need to go.

All of which means that a function like y = e^ix should be fine. Now, we can understand raising a number to a power n as multiplying it by itself n times. This is stretched by such ideas as raising it to a fraction or a negative number, and seems almost to break if the number is imaginary. But the algebra all works, so we’ll let the meaning take care of itself.

Still, how do we evaluate an expression like e^ix? Where do we even start?

We actually have a place to start— the observation from the last section that a good guess at e^i/n is 1 + 1/n. Let’s assume that it’s true for complex numbers as well.

Let’s set n to 1024. That is, a good guess for e^i/1024 is 1 + i/n = 1 + i/1024. That of course is the complex number 1 + .0009765625i.

That gives us one exponential of an imaginary number. (Or rather, an approximation; the actual value ≅ .999999523 + 0.00097656234i.

Given one value of e^ix, here are ways to get more; here’s one. Let’s try for i/512. We could use the 1 + 1/n trick, but it gets less accurate as 1/n gets bigger. Instead, let’s take

e^i/1024 = 1 + .0009765625i

and square both sides. Now, (a^b)^c is always a^bc, so

(e^i/1024)² = e^(i/1024)×2 = e^i/512

For the other side, the general rule for complex numbers is

(a × bi)² = (a × bi)(a × bi)
= a² + 2abi + b²i²
= (a² - b²) + 2abi

Here a = 1 and b = .0009765625, so we get

(1×1 - .0009765625×.0009765625) + 2×1×.0009765625×i
= 0.9999990463 + 0.001953125 i

Let’s see what eⁱⁿ looks like, as a function. (I’m just going to let Wolfram Alpha calculate it.) Here’s how it goes for several values of n.

0 1

.2 0.9800666 + 0.1986693 i

.4 0.921061 + 0.389418 i

.6 0.825336 + 0.564642 i

.8 0.696707 + 0.717356 i

1 0.540302 + 0.841471i

1.2 0.362358 + 0.932039 i

1.4 0.169967 + 0.985450 i

1.6 -0.0291995 + 0.999574 i

1.8 -0.227202 + 0.973848 i

2 -0.416147 + 0.909297 i

2.2 -0.588501 + 0.808496 i

2.4 -0.737394 + 0.675463 i

2.6 -0.856889 + 0.515501 i

2.8 -0.942222 + 0.334988 i

3 -0.989992 + 0.141120 i

3.2 -0.998295 - 0.0583741 i

3.4 -0.966798 - 0.255541 i

It looks like there’s some patterns here. All the values we’ve seen so far, both for the real part and the imaginary part, live between -1 and 1. Moreover, looking down the real column, we see the value smoothly going down; when it reaches -1, toward the end of our list, it inches back up again. The imaginary column goes up, reaches 1, and then declines.

Circling round the subject

Feynman points out something else of note. Simply from the definition of a complex number, we know that

eⁱⁿ = x + iy

Now, a square root always has two solutions, positive and negative. We usually say that √2 is 1.41421356, but we could equally well use -1.41421356. Likewise, if i is √(-1), so is -i. Replacing i with -i in an equation is called taking the complex conjugate, and it gives you another true equation:

e^-in = x - iy

Now let’s multiply these equations together:

eⁱⁿ e^-in = (x + iy)(x - iy)

Simplifying the left side:

eⁱⁿ e^-in = e^{in - in} = e⁰ = 1

And the right side:

(x + iy)(x - iy) = x² +xyi -xyi - i²y² = x² + y²

So for any complex number x + iy that we found as a value of eⁱⁿ, we know that

x² + y² = 1

Does this ring any bells yet? That’s the formula for a circle, so circles are involved in this somehow.

The big reveal

Let’s just get a plot of eⁱⁿ. The red line is the real part, the blue line is the imaginary part.

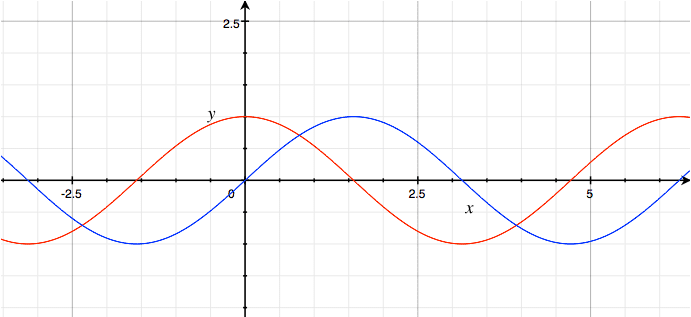
Those look like sine waves. And they are sine waves! In fact we can write

eⁱⁿ = cos n + i sin n

This is the equation Feynman calls the "amazing jewel" of mathematics. We’re just messing around with exponential functions, and we suddenly arrive at the trigonometric functions.

The equation was first published by Leonhard Euler in 1748.

Rather than plotting eⁱⁿ, we can also plot x and y as n varies. We get this graph:

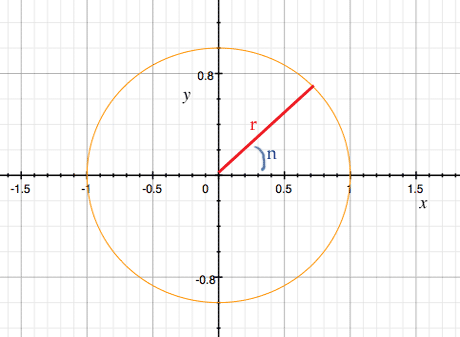
That shouldn’t be surprising, since x² + y² = 1 is how you plot a circle. However, it gives us an alternate way of thinking about eⁱⁿ— we can think of n as an angle, as in the picture. The radius r is also shown, and of course it’s 1.

We can’t represent all complex numbers with eⁱⁿ... but we can represent them as reⁱⁿ. That is, an alternative representation of a complex number x + iy is reⁱⁿ.

Proofs

Maybe it looks like a sine wave but it really isn’t? Well, naturally, there are proofs of Euler’s formula. You can look here, or here, or here.

The problem is that to understand the proofs, you need far more math than is needed just to understand e and sin/cos! Euler himself used the limit expansions of eⁿ, of sine, and of cosine... but even though it’s true, it’s not intuitively obvious that cos x is the sum of -n/(2n)! × x²ⁿ.

Let’s take another approach, along the lines of "use Wolfram Alpha to evaluate limits for us until we’re satisfied we know where this is going". Above I mentioned that Bernoulli’s definition of e was

Now e = e¹, so the general formula is

x can be a complex number, so we can also write

Let’s try a particular value, namely x = π.

For n = 1, this is (1 + iπ/1)¹ = 1 + i π.

You can enter (1 + (i*pi)/2)^2 into Wolfram Alpha, and keep going with higher and higher n’s. Wolfram Alpha will helpfully give you a plot of the results. Here’s how it goes:

It looks like the limit is simply -1, and so it is. Wolfram Alpha will even do limits for you— cut and paste lim((1+(i*pi)/n)^n).

But does Euler’s formula

e^ix = cos x + i sin x

work for x = π? Cos π = -1 and sin π = 0, so yes. π is of course halfway round the unit circle.

Let’s try another number, say π/6, or 30 degrees. Give Wolfram Alpha lim((1+(i*pi/6)/n)^n) and you get ½√3 + ½ i. And this checks out: if you take sin(π/6) you get ½, and cos(π/6) = ½√3.

Now all you have to do is try out every other possible value of x from 0 to 2π. Any number you try, it’ll work.

An example

The good thing about learning your math from Feynman’s lectures is that you almost immediately get a practical application. The bad thing is that to understand the application requires not just following the physical analysis, but having a firm grounding in differential equations.

So to demonstrate the use of complex exponents of e, I’m just going to show one step in a longer derivation. Feynman doesn’t even bother to show the step— he says it’s evident "by inspection"— but I’ll take it a bit slower.

We have a harmonic oscillator (such as a weight held by a spring), driven by a force F, and resisted by friction. The equation is

d²x/dt² + γ(dx/dt) + ω₀²x = F/m

F is itself defined as F₀ cos(ωt + Δ). This makes for a pretty rough differential equation, but here’s where our trick comes in. We pretend that F isn’t a cosine but an exponential, and just ignore the imaginary part. So we use Fe^iωt for the force and xe^iωt for the displacement. (The underlines are reminders that these are complex numbers.) Now the differential equation is

d²xe^iωt /dt² + γ(dxe^iωt /dt) + ω₀²xe^iωt = Fe^iωt/m

Recall that the derivative of e^t is itself. The derivative of e^iωt is almost as easy: bring down the constants, giving iωe^iωt. So the second term

γ(dxe^iωt /dt)

is immediately converted to

γiωxe^iωt

The first term is a double differentiation, which becomes a double multiplication by iω. That is,

d²xe^iωt /dt²

becomes

(iω)² xe^iωt

which reduces to

-ω² xe^iωt

So the differential equation vanishes, replaced by

-ω² xe^iωt + γiωxe^iωt + ω₀²xe^iωt = Fe^iωt/m

If your math is rusty this may not have seemed like an improvement, but again, the clever bit is that we’ve replaced a differentiation with a multiplication, which is far less hairy.

Might as well take the next step: we can divide out e^iωt from both sides:

-ω² x + γiωx + ω₀²x = F/m

Solving for x:

x = F/m(ω₀² - ω² + γiω)

You can see an example of doing all the equations with sine and cosine here, while this page does the same thing with exponentials.

This e^iωt business isn’t just a quirk of weights on springs; it turns up all over. It’s a basic part of analyzing electric circuits; it comes up in tidal effects on the atmosphere; it pops up in nuclear physics. Nature is lazy, and uses the same damn equations for everything.

1/n	e^1/n	1 + 1/n
1	2.7182818	2
1/2	1.648721271	1.5
1/4	1.2840254	1.25
1/8	1.133148453	1.125
1/16	1.06449446	1.0625
1/32	1.0317434075	1.03125
1/64	1.015747709	1.015625
1/128	1.007843097	1.0078125
1/256	1.003913889	1.00390625
1/512	1.00195503	1.001953125
1/1024	1.000977039	1.0009765625
1/2048	1.000488400	1.00048828125

0	1
.2	0.9800666 + 0.1986693 i
.4	0.921061 + 0.389418 i
.6	0.825336 + 0.564642 i
.8	0.696707 + 0.717356 i
1	0.540302 + 0.841471i
1.2	0.362358 + 0.932039 i
1.4	0.169967 + 0.985450 i
1.6	-0.0291995 + 0.999574 i
1.8	-0.227202 + 0.973848 i
2	-0.416147 + 0.909297 i
2.2	-0.588501 + 0.808496 i
2.4	-0.737394 + 0.675463 i
2.6	-0.856889 + 0.515501 i
2.8	-0.942222 + 0.334988 i
3	-0.989992 + 0.141120 i
3.2	-0.998295 - 0.0583741 i
3.4	-0.966798 - 0.255541 i